1. 量子物理的概率世界
我们所处的世界是概率的。理解这个世界最好方式就是薛定谔的猫的思想实验。
- 首先了解一下原子的衰变。一些原子有性质叫“半衰期”,是一个时间为单位的量。比如A原子半衰期10年是说,N个A原子经过十年会有一半发生衰变反应。
- 但是原子的衰变是概率的。N个A原子中每一个原子进行衰变都是概率的,也就是我们无法确定是哪一半A原子会发生衰变。
- 如果一直盯着一个原子看,会怎么样呢?我们可以挑选一些半衰期短的原子,对一个个原子持续的观测,看看能不能捕捉到它衰变的瞬间。但是目前的实验发现,科学家持续观测的那一个原子,一直不会发生衰变。
- 有一种解释是说,原子的状态是概率的,但是观测会让它的概率坍缩。或者说,科学家进入了那个概率的没有衰变的原子所处的世界。不过在观测前,原子的状态还是概率的,它同时衰变了、但又没有衰变,虽然我们可以量化它每种状态的概率。
- 那如果有那有一个装置“将”会对某一个原子进行观测,“如果”观测到原子坍缩了,就会往装着猫的黑盒子释放毒气,杀死猫;否则就什么都不做。那猫的生死就紧紧和原子的状态耦合在一起了,猫也就处在一个概率的状态。
- 虽然我们也可以量化的表示猫生或死的状态。但是无论概率是多少,打开盒子的那一刻(我们和猫和原子的状态耦合在一起的一刻)、我们可能处在猫生的状态,也可能处在猫死的状态。
这样的观点下,我们的世界也是概率的,虽然我们可以量化的描述一些概率,但是最终我们会进入哪一个状态,没有人能够预测。
2. 非线性混沌系统
另外,还有混沌系统。简单来说,就是一个动力学系统(随时间变化的状态),初始的状态只要发生了极其微小的变化、这一点点差异可以迅速被无限放大。也就是蝴蝶效应。这也展示了数学理性的范围。而我们生活中的几乎所有的系统都是混沌的。
举一个简单的混沌的例子,来方便理解。 google colab link
def update_function(x):
return x * x + x - 1
def render_frame(rescale_factor = 1.0, center = [0, 0]):
interval_tmp = interval * rescale_factor
axis_x = np.linspace(-interval_tmp,interval_tmp,resolution) + center[0]
axis_y = np.linspace(-interval_tmp,interval_tmp,resolution) + center[1]
X,Y = np.meshgrid(axis_x,axis_y)
Z = X + Y*1j
for i in range(num_iteration):
Z = update_function(Z)
return colorize(Z)
描述的是在复数空间中‘update_function’迭代,对于不同的初值,最终收敛到的值。

- 可以发现在某些地方,初值只要稍稍变动,就会得到完全不同的最终收敛值(可能是0和无限的差别)。这就是所谓的蝴蝶效应,一个非常小的变化,可能导致天翻地覆的变化。
- 可能有人会提出计算机的发展能不能解决这个问题。答案是不能,计算机的发展可以使得我们的浮点数的精度提高,比如说我们可以计算到小数点后面N位,发展到可以计算2N位,但是我们可以把混沌分形的图放大无限倍,但是它的“性质”还是一样的。“三体”问题也是一个同样的混沌系统,再精密的计算机也不能预测它的未来,就在于这一点。
- 虽然混沌、无法预测,但是它绝对不是一团乱麻一片虚无。就像图里可以看到的,它有特殊的美妙的图像、规律。我们虽然什么都不能预测,不能量化分析一切,但是我们可以领会到其中的规律。
3. 其他
另外关于人脑,据说有一些研究发现神经元之间的鞘有一些量子物理的特性。所以我觉得传统计算机不可能模拟出人脑,但是量子计算机有可能。人脑是一个参数量硕大的动力系统,它一定也是混沌的,优美有序但是无法预测的。我也觉得混沌中的秩序,与有机的生命、与我们的意识,有甩不清的关系。
4. 量子力学与物质的客观实在性
量子力学:用概率的波函数描述粒子。
当今时代,量子信息技术发展突飞猛进,给人们传统的物质观念带来很大冲击。在经典物理学中,微观粒子是彼此分立的,既有质量和体积,也有时空定位,其运动有轨迹可循。微观粒子的相互作用可观察、可感知、可表征,不受观测主体影响。微观粒子能量的释放和传播是连续的、无限可分的。
描述经典物理的观点:分立的原子,连续的能量和状态。
然而“量子”概念的确立,意味着微观粒子的运动不再像宏观物体运动那样有确定的轨迹,其运行具有概率性质,其能量释放和传播是不连续的。
量子物理的一个性质,就是能量的单元——用普朗克常数$\hbar$规定的——一个光子的能量$\hbar \nu$。这个又是和测不准定理uncertainty principle——粒子的位置與動量不可同時被確定——相关联的。
\[\delta_x \delta_p \le \frac{\hbar}{2}\]因为测量的过程都是物质间的相互作用,比如光子、粒子的碰撞。但是相互的作用会影响到测量物的状态,所以为了测量更精细的量,我们需要用更小的能量单元去碰撞。但是由于能量单元是有限制的,所以我们能够测量的最精细的量也是有限制的。而一般情况下,位置用来测量动量,动量用来测量位置,所以“粒子的位置與動量不可同時被確定”。
微观粒子具有波粒二象性,其存在可以用严格的数学形式加以描述,性质非常独特:既能产生又能湮没,可以从碰撞过程所包含的能量中创生出来,这对传统的“物质无限可分”观念提出了新的挑战。
波粒二象性来自于一些粒子的实验,比如我们发现在高速状态下电子也表现出和光波一样的性质——干涉和衍射。而光也能够在某些情况下,表现出粒子的性质。
- 量子的真空是沸腾的。间接证据:黑洞发光。
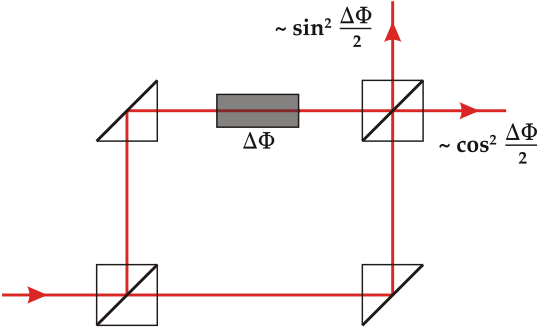
- 干涉实验中的量子特性。Mach–Zehnder interferometer.
- 粒子的衰变。
曾经相互作用过的两个粒子,不管分离之后相距多远,始终会神秘地联系在一起,其中一方发生变化,就会立即引发另一方产生相应的变化(这种现象被称为“量子纠缠”,且这种纠缠可以被调控)。
- 假设薛定谔的猫,在没有打开盒子的情况下,把原子拿出来分隔。那么猫和那个量子就构成了纠缠。
测量方式影响微观粒子被测量时的状态,实验结果随着测量环境的变化而变化。量子力学的发展表明,在徵观领域内不能像经典物理学那样理解“实在”,不能离开人的存在和观测的影响而抽象地谈论微观世界的“实在”。
- 一个理解方式是测不准定理。测量是一个交互作用,测量的操作一定会影响被测量的量。
- 另一个理解是,观测者似乎在量子力学系统中有很大的作用,观测能够导致概率的坍缩。
但是,量子的特性并没有否定物质的客观实在性,量子纠缠也不是一种精神现象。微观粒子仍然是一种真实的“容观实在”,而量子力学只是揭示了它以什么方式 “真实存在”。客观实在之“客观”是在不依赖于人的意识而存在的意义上讲的。
- 最终,波函数的描绘还是符合实验结果的。