Quantum Computing For Everyone - An Introduction, Certification link.
1. History, Theory, and Basics
1.1 History
- Transistor Invention (1947): John Bardeen, William Shockley, and Walter Brattain invented the transistor, which paved the way for technological advancements.
- Quantum Mechanics Foundations:
- Ernest Rutherford (1909): Introduced the atomic model with a dense nucleus.
- Niels Bohr (1913): Proposed a quantum model of the atom with quantized energy levels.
- Max Planck (1900): Introduced the concept of energy being emitted in discrete units (quanta).
- Albert Einstein (1905): Developed the photoelectric effect theory, linking light to quantized energy.
- Advancements in Quantum Theory:
- Heisenberg (1925): Formulated matrix mechanics and the uncertainty principle.
- Erwin Schrödinger: Developed wave mechanics, describing particles as wave-like entities.
- Richard Feynman’s Contribution (1981): Proposed the idea of quantum computers to efficiently simulate quantum phenomena, highlighting the limitations of classical computers.
- Theoretical Advances (1980s-1990s): Researchers like David Deutsch and Peter Shor laid the groundwork for quantum algorithms and cryptography.
1.2 Theory
- Qubits: The Building Blocks.
- Quantum Gates and Circuits, fundamental operations that manipulate qubits.
- Quantum Algorithms. e.g. Shor’s Algorithm, Grover’s Algorithm.
- Technical Challenges:
- Qubit Stability
- Quantum Error Correction
- Scalability
𐙚‧₊˚📜✩ ₊˚⊹♡ Readings:
- Quantum Computation and Quantum Information” by Michael A. Nielsen and Isaac L. Chuang.
- “Introduction to Quantum Mechanics” by David J. Griffiths and Darrell F. Schroeter.
- The Mathematics of Quantum Mechanics
- Preliminary Mathematics for Quantum Computing
- Quantum Computing - Peter W. Shor
- The Mathematics Behind Quantum Computing: Part I
- The Mathematics Behind Quantum Computing: Part II
1.3 Quantum Mechanics
Superposition; Quantum Interference; Entanglement.
- Introduction to quantum mechanics
- Quantum Mechanics For Beginners
- Quantum Computers, Explained With Quantum Physics
2. Building Blocks of Quantum Computing
2.1 Qubits
- Duality of Matter
- Bra & Ket.
- The Bloch Sphere and Basis States
- Mach-Zender Interferometer
Decoded How Does a Quantum Computer Work?
2.2 Gates and Circuits
Quantum Computing Concepts – Quantum Logic. Classical and Quantum Gates. 🌺 Quantum Computing Simulators.
- classic gates : AND, OR, XOR (irreversible), form a universal set.
- XOR ($\oplus$) is equivalent to x+y(mod2) operation.
- unitary operator : quantum gates must be reversible (no information is lost).
- CNOT (controlled-NOT) gate (reversible). \(\begin{pmatrix} x \\ y \end{pmatrix} \to \begin{pmatrix} x \\ x \oplus y \end{pmatrix}\)
- Quantum Circuit : Each qubit is represented by a line in the circuit diagram and time runs from left to right.
- Gates and circuits are linear.
- No loop, cannot splay out, cannot merge.
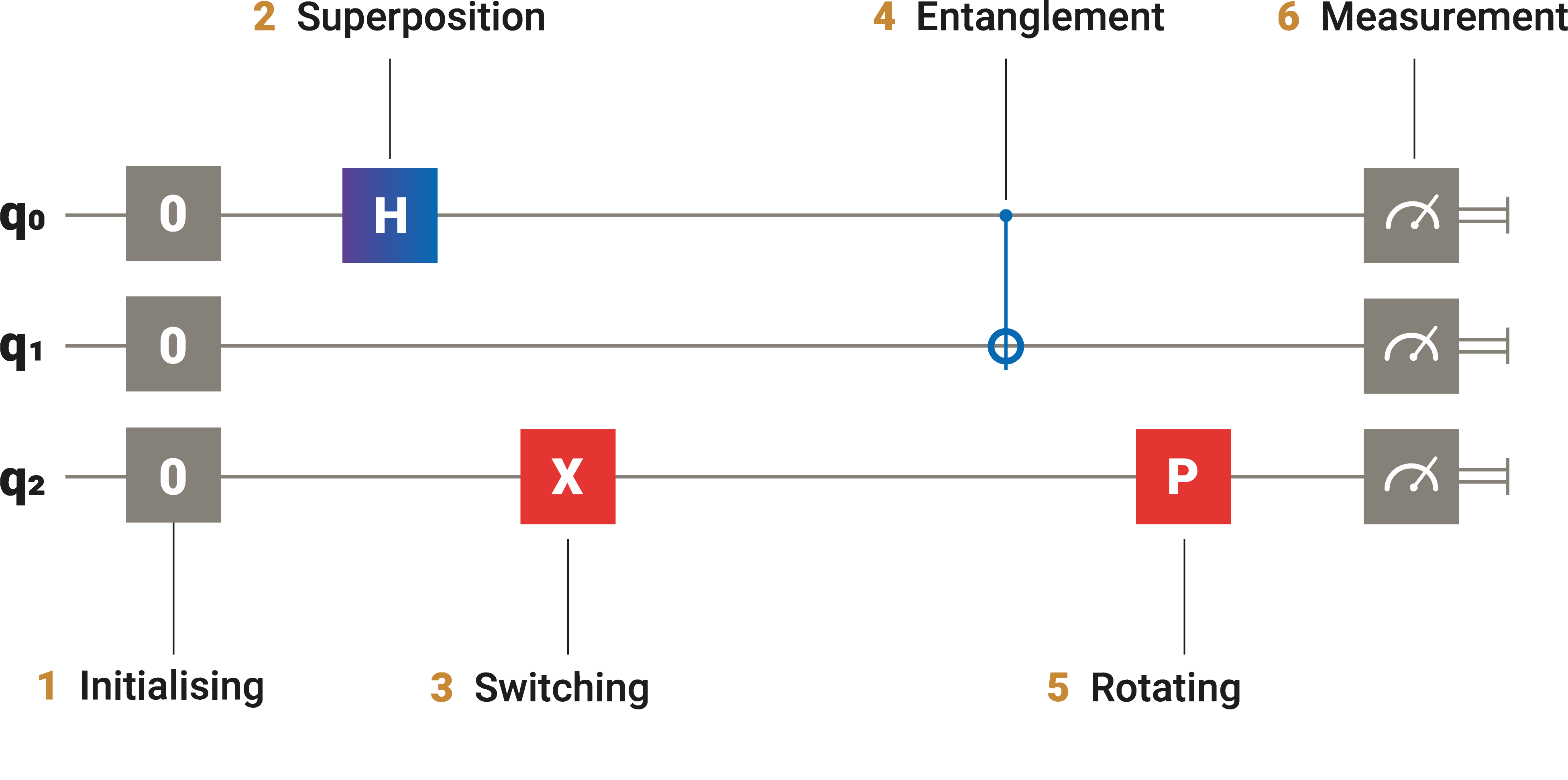
- Quantum gates are unitary operators and so must be reversible.
- single-qubit unitary gates
- NOT gate (Pauli X) : \(X =\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\)
- Phase flip gate (Pauli Z) : \(Z =\begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix}\)
- Pauli Y : \(Y =iXZ=\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}\)
- Hadamard gate: \(H =\frac{1}{\sqrt 2}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}\)
- General 2×2 unitary matrix : \(A = a_{0}I + a_{x}X + a_{y}Y + a_{z}Z\).
- Measurement Gate.
- CNOT (two qubits gates): \(U_{CNOT} = \begin{pmatrix} I & 0 \\ 0 & X \end{pmatrix}\)
- CNOT gates, along with single-qubit unitary gates, form a universal set for quantum computation.
- single-qubit unitary gates
2.3 Classical vs. Quantum
Classical And Quantum Logic,Gates,Transistors and Computing
1. Classical vs. Quantum Logic
| Feature | Classical Logic | Quantum Logic |
|---|---|---|
| Basic Concept | Based on binary values (true/false) and definite states | Based on probability distributions and quantum states |
| Principle | Law of the excluded middle (a statement is either true or false) | Superposition (a state can be both true and false simultaneously) |
| Handling Uncertainty | Limited; cannot handle uncertainty or vagueness well | Handles uncertainty and probability inherently |
| Formal Systems | Propositional logic, predicate logic | Quantum mechanics framework |
| Applications | Philosophy, mathematics, computer science | Quantum computing, quantum information theory |
2. Classical vs. Quantum Gates
| Feature | Classical Gates | Quantum Gates |
|---|---|---|
| Basic Concept | Process binary inputs (0 or 1) to produce binary outputs | Operate on qubits (quantum bits) and enable superposition and entanglement |
| Common Types | AND, OR, NOT, NAND, NOR, XOR, XNOR | Single-qubit gates (e.g., NOT, Hadamard), multi-qubit gates (e.g., CNOT, SWAP) |
| Output Determinism | Deterministic; output is fixed for given inputs | Probabilistic; output depends on quantum state and measurement |
| Reversibility | Most classical gates are irreversible (e.g., AND, OR) | Quantum gates are reversible (unitary operations) |
| Applications | Digital circuits, memory circuits, arithmetic circuits | Quantum circuits, quantum algorithms, quantum error correction |
3. Classical vs. Quantum Transistors
| Feature | Classical Transistors | Quantum Transistors |
|---|---|---|
| Basic Concept | Three-terminal device (source, drain, gate) controlling current flow | Manipulate quantum states of electrons to control current flow |
| Operation | Use electric field to control current between source and drain | Use quantum mechanics principles to enable superposition and entanglement |
| Information Unit | Binary digits (bits) | Quantum bits (qubits) |
| Performance | Suitable for classical computing; limited by binary nature | Potentially faster due to parallel processing; suitable for quantum computing |
| Challenges | Scalability limited by physical size; heat dissipation | Fragility of quantum states; error susceptibility; requires advanced technologies |
| Applications | Classical computers, digital devices | Quantum computers, quantum communication systems |
4. Classical vs. Quantum Computing
| Feature | Classical Computing | Quantum Computing |
|---|---|---|
| Basic Concept | Based on classical logic and binary arithmetic | Based on quantum mechanics and qubits |
| Information Unit | Binary digits (bits) | Quantum bits (qubits) |
| Computation Model | Sequential processing; limited by binary nature | Parallel processing; exponential growth in computational power |
| Handling Uncertainty | Limited; not suitable for probabilistic tasks | Handles uncertainty and probability inherently |
| Applications | General-purpose computing, office applications, complex simulations | Cryptography, drug discovery, optimization, artificial intelligence, quantum simulations |
| Current State | Well-established; widely used in daily life | Emerging technology; still in development stage |
| Future Potential | Limited by physical constraints | High potential for revolutionizing various fields; still facing technical challenges |
2.4 Hardware
- Superconducting Qubits: Widely used, relying on superconducting circuits at low temperatures, allowing for easy fabrication and scalability. Companies like IBM and Google are leading in this area.
- Trapped Ions: Utilize individual ions manipulated by lasers for high fidelity operations and longer coherence times, with companies like IONQ making significant progress.
- Photonic Quantum Computing: Uses photons for encoding and processing information, ideal for communication applications. Companies like Xanadu are exploring this technology.
- Topological Quantum Computing: Based on exotic particles called anions, which are resistant to errors. Microsoft is a key player in this field.
- Analog Quantum Computing: Focuses on evolving quantum systems over time to find optimal solutions, with D-Wave systems pioneering this approach.
- Quantum Computer Components: Discusses the quantum data plane, control processor plane, and host processor, which are essential for managing qubit states and processing information.