Chaos is aperiodic long-term behavior in a deterministic system that exhibits sensitive dependence on initial conditions.
1. Simulations
1.1 Infinite-period Bifurcation
\[\begin{align*} & \dot{r} = r(1 - r^{2}) \\ & \dot{\theta} = \mu - sin\theta \end{align*}\]1.2 Lorenz Attractor
\[\begin{align*} & \dot{x} = a(y - x) \\ & \dot{y} = x(b - z) - y \\ & \dot{z} = xy - cz \end{align*}\]One commonly used set of constants is a = 10, b = 28, c = 8 / 3. Another is a = 28, b = 46.92, c = 4. “a” is sometimes known as the Prandtl number and “b” the Rayleigh number.
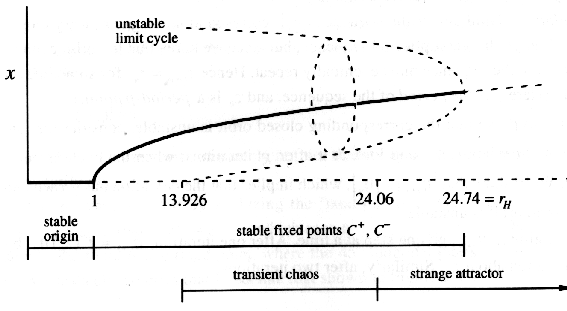
- $ 0 < \rho \le 1$ : 0 is the asymptotically stable critical point - the system converges to zero.
- $ 1 < \rho < 13.926 $ : Depending on the initial values, the solution will quickly converge to one of the critical points.
- $ \rho = 13.926 $ : homoclinic explosions. a complicated invariant set is born.
- $ 13.926<\rho<24.06 $ : transient chaos, the system is not “chaotic”, because long-term behavior is not aperiodic. On the other hand the dynamics do exhibit sensitive dependence on initial conditions.
- $ 24.06<\rho<24.74 $ : two types of attractors : fixed points and a strange attractor. (large perturbation can knock from one to another).
- $ \rho > 24.74 $ : The famous Lorenz attractor!
- $ \rho ≈ 99.65 $ : There is a stable 6-period orbit in the form $a^{2}ba^{2}b$.
- $ \rho ≈ 100.75 $ : There is a stable 3-period orbit $a^{2}b$, that is it spirals around one critical point once and the other twice.
- $ \rho > 313 $ : has a globally attraction limit cycle.
exhibit stretching and folding of trajectories
1.3 Logisitic Map
\[x_{n+1} = rx_{n}(1 - x_{n})\]If the system’s Lorenz map is nearly one-dimensional and unimodal, then the universality theory applies.
2. Fractal
Demos:
- C has structure at arbitrarily small scales.
- C is self-similar.
- The dimension of C is not an integer.
3. Philosophy
Chaos - Stanford Encyclopedia of Philosophy
3.1 Quantum Chaos
Quantum Chaology: “the study of semiclassical, but nonclassical, phenomena characteristic of systems whose classical counterparts exhibit chaos”.
| classical chaotic dynamics | quantum dynamics |
|---|---|
| the state space supports fractal structure | the state space does not support fractal structure |
| bounded macroscopic systems, continuous energy spectrum associated with its motion | bounded, isolated systems, discrete energy spectrum associated with its motion |
Some limitations :
- Schrödinger’s equation is linear, quantum states starting out initially close remain just as close (in Hilbert space norm) throughout their evolution - no stretching and folding mechanism in the system space.
- Phenomena such as SDIC (sensitive dependences on initial conditions) could only be possible in quantum systems that appropriately mirror classical system behaviors
- Semi-classical quantum systems could be expected to mirror the behavior of their corresponding classical systems only up to the Ehrenfest time, of the order ln(2π/h) secs. (Berry et al. (1979))
- two effects at work in semi-classical systems over time: (1) the coalescing of classical chaotic trajectories and (2) the spreading of quantum wave packets.
Some Broader Implications of Chaos:
- Chaos and Determinism. chaos : unpredictability in deterministic system.
- Free Will and Consciousness.
- local context (particle trajectories) : quantum effects affecting the outcomes of human choices.
- but how quantum mechanics itself and measurements are interpreted as well as the status of indeterminism?
- global context : arrangements of the particles are the fundamental explanatory elements and not the individual particles and trajectories.
- which are generally irreversible with respect to time.
- nonlinear nonequilibrium models also exhibit SDIC.
- local context (particle trajectories) : quantum effects affecting the outcomes of human choices.
- Human and Divine Action in a Nonlinear World, apply NDS theory to complex behavior.