Table of Contents

Summary

Deep Learning

More Work are done with Deep Learning.

TUM AI Lecture Series - Image-based Rendering.

LLFF: Local Light Field Fusion: Practical View Synthesis with Prescriptive Sampling Guidelines, github

1. Neural Rendering

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis 2020. MLP taking in a 5D coordinate and outputting density and color. Trainning a map : $F_{\Theta}(x, d) \to (x, \sigma)$ , from the pixel ray - defined by x (optical center), d (direction), to volumn density and color. Each pixel ray will be sampled to 'N_sample' points, each point run the network, then integrated to get the final value.

        graph LR
        A[Position of point] --> B[MLP encoder]
        B --> C[FCxN]
        C --> D[FC]
        B --> D
        D --> E[FCxN]
        E --> F
        X[Direction of ray] --> Y[MLP encoder] --> F[FC]
        F --> G[RGB & sigma]
        style A fill:#f9f,stroke:#333,stroke-width:4px
        style X fill:#f9f,stroke:#333,stroke-width:4px
        style G fill:#bbf,stroke:#333,stroke-width:4px
  • Need times to train for each data session.
  • Train LLFF dataset (“forward-facing” scenes) in “normalized device coordinates” (NDC) space; large rotation scene in conventional 3D world coordinates.
  • google jaxnerf implementation, see here with my tests.

NERF Extension:

NERF Acceleration:

Pointcloud representation:

Gaussian Splatting Details
  • Anisotropic covariance: use scale vector and rotation to model (to ensure covariance being positive semi-definite).
  • Tile-based rasterizer for feat optimization, github code. Following previous work : Pulsar.
  • Other work : point-based neural rendering (who project neighbor views and use NN to optimize the fused MVS view).
  • D - Structural SIMilarity (SSIM) image loss (introduced in "Structural Similarity-Based Object Tracking in Video Sequences").
  • Use degree 3 SH, while PlenOctrees uses degree 2. and from the tests, SH requires lost of parameters, while produce little improvement.
  • Unity3D tool for gaussian splitting rendering., it also simplifies the SH to reduce memory consumption.
  • Web visualization.
    • 4D Gaussian Splatting. Add MLP for each point along with time, to produce video. 3DGS is completely explicit, while this paper make it partly implicit, I don't like this degrade.
    • 4D4K 2023. 4D grids representations. I think a 4D pcl represented GS will be simply better.
      • initialized by space-caving for each timestamp from multi-view images.
      • geometry: radius, density, position. (isotropic version of 3DGS)
      • color: blending model + MLP SH. (Need MLP for each point.)
      • render: (for each pixel) take k nearest points and merge by density. (No alpha blending.)
    • Dynamic 3D Gaussians: Tracking by Persistent Dynamic View Synthesis, save point positions & rotations for each timestamp (while scale, and render parameters are shared) - rigid point motion.
      • problems : need simultaneously multi-view collection, and save pcl for each timestamp is memory consuming.

    A generalization of the problem:

    Instant Neural Graphics Primitives 2022 - An object represented by queries to a nerual network. git page. Train & render NeRF in realtime, and enable various of GUI to interact & visualize & edit.

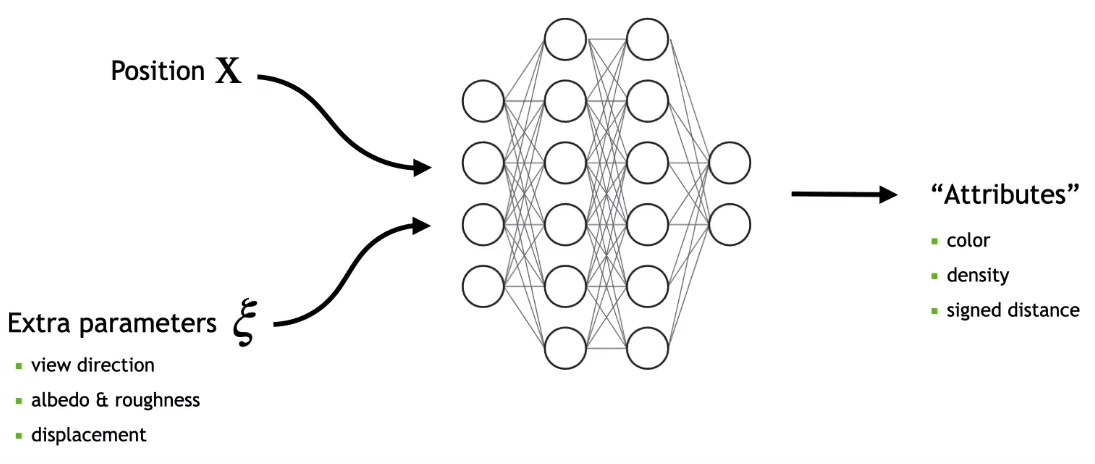
    • Examples :
      • GigaPixel Image : 2d position X (in image) -> RGB color.
      • SDF : 3d position X -> distance to surface.
      • Nerf : 3d position X + view direction d -> RGB color & density.
      • Radiance Caching : 3d position X + Extra parameters -> RGB color global illumination.
    • Acceleration Design :
      • Nerf render process: cut empty space, and cut ray after object.
      • Smaller MLP: memery traffic dominate -> Fully Fused Neural Network : entire neural network implemented as single CUDA kernel.
      • Input encoding (see understanding of input encoding): Multireslution hash encoding - pyramid structure for deep features (use hash to avoid dimensionality exponentially as in the hyper-cubical voxel case).
    • here for my test results, run with a outdoor general data session.

    2. SDF

    PermutoSDF: Fast Multi-View Reconstruction with Implicit Surfaces using Permutohedral Lattices 2023, github page, github. (1) use a hashed permutohedral encoding(following Instant NGP) to ensure fast training; (2) a novel RGB regularizer to encourage the network to predict high-frequency geometric detail.

    NeuS2: Fast Learning of Neural Implicit Surfaces for Multi-view Reconstruction 2023, following work of Instant NGP.

    • multi-resolution hash tables of learnable feature vectors.
    • an incremental learning method for learning dynamic scenes.

    Occupancy Network.

    Improving neural implicit surfaces geometry with patch warping 2022, github.

    VolSDF: Volume Rendering of Neural Implicit Surfaces 2021, github. define the volume density function as Laplace’s cumulative distribution function (CDF) applied to a signed distance function (SDF) representation. model the density:

    \[\sigma(x) = \alpha \Phi_{\beta}(-d_{\Omega}(x))\] \[\begin{equation} \Phi_{\beta}(s) = \begin{cases} \frac{1}{2}exp(\frac{s}{\beta}) & \text{if $s \le 0$}\\ 1 - \frac{1}{2}exp(-\frac{s}{\beta}) & \text{if $s > 0$} \end{cases} \end{equation}\]
    • MLP1. sdf d and feature z: $f_{\phi}(x) = (d(x), z(x)) \in R^{1+256}$
    • MLP2. scene’s radiance field: $L_{\phi}(x, n, v, z) \in R^{3}$

    Implicit Neural Representations with Periodic Activation Functions 2020. A continuous implicit neural representation using periodic activation functions that fits complicated signals. Solve challenging boundary value problems.

    \[F(x, \Phi(x), \triangledown_{x}\Phi, \triangledown_{x}^{2}\Phi, ...) = 0\]
    • ReLU networks are piecewise linear incapable of modeling higher-order derivatives. While alternative activations are not well behaved.
    • SIREN: $\Phi(x) = W_{n}(\phi_{n-1} \circ \phi_{n-2} \circ … \circ \phi_{0})(x) + b_{n}$, $x_{i} \to \phi_{i}(x_{i}) = sin(W_{i}x_{i} + b_{i})$. The activations of Siren always alternate between a standard normal distribution with standard deviation one, and an arcsine distribution.
    • $\Phi(x)$ being a FC, loss be the $\int_{\Omega} \sum_{i}I_{\Omega_{i}}(x)|F(x)| dx$. ($\Omega_{i}$ is a sampling)
    • Poisson Equation, SDF(+-1), Helmholtz and Wave Equation. github.
    • Compared with NERF pose encoding in github.

    DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation 2019 DeepSDF network outputs SDF value at a 3D query location. Shape completion (auto-decoding) takes considerably more time during inference. github.

    3. Multi-View Geometry

    Multi-View Stereo

    PatchmatchNet: Learned Multi-View Patchmatch Stereo, github. checked in a few scenes, and run fusion the pointcloud, not ideal.

    Mulit-View Interpolation

    IBRNet: Learning Multi-View Image-Based Rendering 2021. Start from the target view and interpolate nearby source images (instead of encode the whole model - NERF) (similar to traditional MVS pipeline) : (1) select neighbor (source) images; (2) sample depths in each ray, project to the source images; (3) aggregate the source 2d features; (4) synthesis by a Ray Transformer. (But quality slightly worse than NERF).

    Light Field Neural Rendering, google post. uses a lightfield parameterization for target pixel and its epipolar segments in nearby reference views.

    2022

    ACMMP : Multi-Scale Geometric Consistency Guided and Planar Prior Assisted Multi-View Stereo, following work of ACMM, using planar prior.

    2021

    Voxel Structure-based Mesh Reconstruction from a 3D Point Cloud, github code. It has a classification of meshing methods:

    • Approcimation-based method: Poisson, MLS(moving least squares), Scale Space. Rebuild the 2-manifold mesh to fit a point cloud directly. while may loss local details.
    • Delaunay-based method: point connection, require ideal point cloud distribution.
    • Point Resampling: resample a point cloud into an isotropic one (then we could apply Delaunay).
    • Pre- and Post-processing: mesh denoising, isotropic remesh and mesh repair.

    This paper’s method contains the following steps:

    • pre-treatment : moving least squares smoothing point cloud. delaunay based interpolation to make isotropic point cloud.
    • make voxel structure: based on geodesic distance.
    • make mesh: resample points in each voxel (using Farthest Point Sampling, and apply dyanmic resample rate), then apply delaunay.

    Efficiently Distributed Watertight Surface Reconstruction the distribution of all the steps (Delaunay + graph-cut).

    Dense Surface Reconstruction from Monocular Vision and LiDAR LiDAR measurements are integrated into a multi-view stereo pipeline for point cloud densification and tetrahedralization. (the lidar mapping algorithm it used seems terrible, our algorithm is much much better)

    2020

    Deep Local Shapes: Learning Local SDF Priors for Detailed 3D Reconstruction replace traditional signed distance function with neural network.

    Point2Mesh: A Self-Prior for Deformable Meshes using DL method (Neural Self-Priors) iteratively shrink-wrap the initial mesh, leading to a watertight reconstruction (fits the point cloud).

    A 3D Surface Reconstruction Method for Large-Scale Point Cloud Data nothing new.

    2019

    Detail Preserved Surface Reconstruction from Point Cloud (noise image based point cloud) a new Visibility Model : $(1-e^{d^{2}/2 \sigma^{2}})$.

    ACMM Multi-Scale Geometric Consistency Guided Multi-View Stereo, github.

    • multi-scalar process to handle low texture area.
    • Adaptive checkerboard propagation (~ more complicated DSO pattern).
    • used in our project, has good and fast result. but poor in close repeated pattern (close ground), (might be fixed by plane prior in their following work ACMMP).

    2018

    Reconstructing Thin Structures of Manifold Surfaces by Integrating Spatial Curves. use image based 3d curve reconstruction to enhance thin structures.

    • compute 3D curves based on the initialize-optimize-extend strategy.
    • Curve-conformed Delaunay Refinement to preserve thin structures: make sure Delaunay has kept all the segments of curves, and close region has finer triangles. Add sepcial energy to tetrahedra belonging to the same curve.

    2017

    Voxblox: Incremental 3D Euclidean Signed Distance Fields for On-Board MAV Planning, github code. state of art, TSDF, ESDF, and meshing. Extremely efficient!, wonderfully engineering art. (I had been using it for several years)

    2016

    A Survey of Surface Reconstruction from Point Clouds. The Role of Priors :

    Surface Smoothness :

    Visibility:

    Volume Smoothness : enforce that the local shape thickness of a surface (i.e. a measurement of its local volume) varies smoothly to fill incomplete point cloud.

    Geometric Primitives: (scene geometry may be explained by a compact set of simple geometric shapes), good for indoor and CAD models (both have samller range).

    Global Regularities : CAD models, man-made shapes and architectural shapes – possess a certain level of regularity. Structure-aware shape processing 2013.

    Data-driven priors (semantic objects) : using a collection of known shapes to help perform reconstruction.

    • Scene reconstruction by rigid/non-rigid retrieval.
    • Object reconstruction by part composition.
    • Reconstruction in shape spaces.

    User-Driven Methods : Topology cues, Structural repetition cues, Primitive relationship cues, Interleaved scanning and reconstruction.

    Evaluation of Surface Reconstruction: Geometric Accuracy, Topological Accuracy, Structure Recovery, Reproducibility

    Earlier

    Superpixel meshes for fast edge-preserving surface reconstruction 2015 superpixels and second-order smoothness constraints. based on Single-view 3D mesh reconstruction: 2D base mesh extraction, Depth reconstruction, then point cloud and mesh.

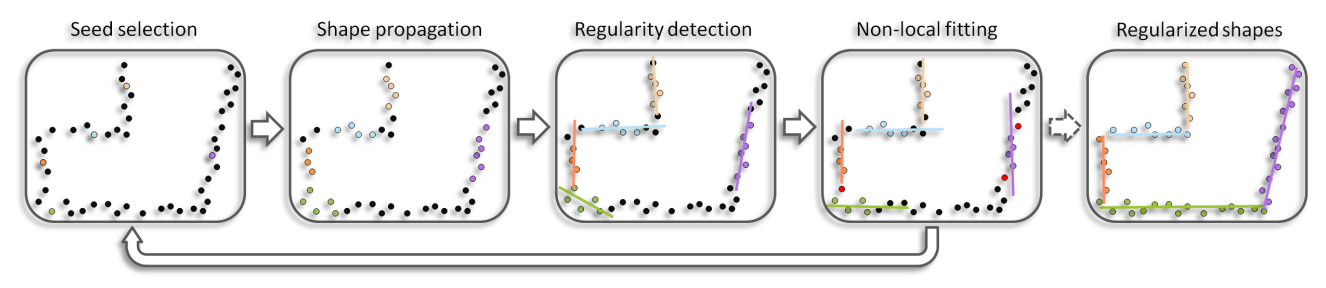
    Planar Shape Detection and Regularization in Tandem 2015 automated detection and regularization of primitive shapes from unorganized point clouds. And enforcing parallel and orthogonality constraints in the detection of planes. repeating the following:

    • uniformly distributed seeds, region grow, detect primitive shapes.
    • regularization and adjust coplanarity.

    Let There Be Color! Large-Scale Texturing of 3D Reconstructions 2014, github code view selection then project to get texture. It performs well in our image mapping mesh result (using poisson). While it has high requirement on the mesh. Tested with some lidar mapping point cloud (made with TSDF + matching cube, without further de-noise), the result mesh is terrible. I presume it is caused by loss of accuracy in TSDF, and noise in lidar data.

    Surface Reconstruction through Point Set Structuring 2013.

    • structuring and resampling the planar components into planar, crease(to connect adjacent primitives), corner and clutter.
    • reconstructing the surface from both the consolidated components and the unstructured points.
    • surface is obtained through solving a graph-cut problem formulated on the 3D Delaunay triangulation (see this part for more details). Following by a Surface quality refinement and simplification.

    Watertight Scenes from Urban LiDAR and Planar Surfaces 2013

    • make into small region.
    • conforming constrained Delaunay tetrahedralization (CCDT) to partition 3-dimensional space into tetrahedral cells. (details to read)
    • minimum-weight graph-cut. see more

    Real-time 3d reconstruction at scale using voxel hashing.

    2.5D Building Modeling by Discovering Global Regularities 2012:three fundamental type of relationships in buildings (for reconstruction from Aerial imagery):

    • roof-roof relationships that consist of orientation and placement equalities.
    • roof-roof boundary relationships that consist of parallelism and orthogonality relationships.
    • boundary-boundary relationships that consist of height and position equality.

    finding the relationships via clustering (i.e., clustering similar angles, equality, etc..), they are used to inform the primitive fitting method so that the primitives simultaneously fit to the data and to the relationships.

    GlobFit: Consistently Fitting Primitives by Discovering Global Relations 2011 assuming man-made engineering object, RANSAC -> Find global relationship -> alignment (merge close elements in the orientation space). Starting from an initial set of detected primitives, parallel, orthogonal, angle-equality, and distance-equality relation-ships are individually detected and carefully selected so as to not cause any relationship conflicts.

    Multi-view reconstruction preserving weakly-supported surfaces 2011. Some papers refer this as state-of-art.

    • baseline (the following paper) constant point weight.
    • point weight depends on the number of observations, make a filter strategy for the initial Delaunay. (closer to the colmap implementation)
    • a free-space-support weight function. compute all weights in the same way as the base-line approach. Then search for all large jumps and multiply the corresponding t-edge weights. (good for noisy data, need to test)

    Robust and efficient surface reconstruction from range data 2009 formulates of the surface reconstruction problem as an energy minimisation problem that explicitly models the scanning process. Uses Delaunay triangulation to formulate as a graph cut problem using line of sight information: labeling interior/exterior. (colmap uses its implementation).

    • minimum cuts for optimal surface reconstruction :
      • removing the edges connecting two sets of vertices, that is finding two disjoint sets S and T,
      • with a cost: the sum of the capacities of the edges going from S to T.
      • same as computing the maximum flow from the source s to the sink t.
    \[c(S, T) = \sum_{v_{i} \in S \setminus \{s\} \\ v_{j} \in T \setminus \{t\}} w_{ij} + \sum_{v_{i} \in S \setminus \{s\}} t_{i} + \sum_{v_{i} \in T \setminus \{t\}} s_{i}\]
    • Surface visibility: soft visibility
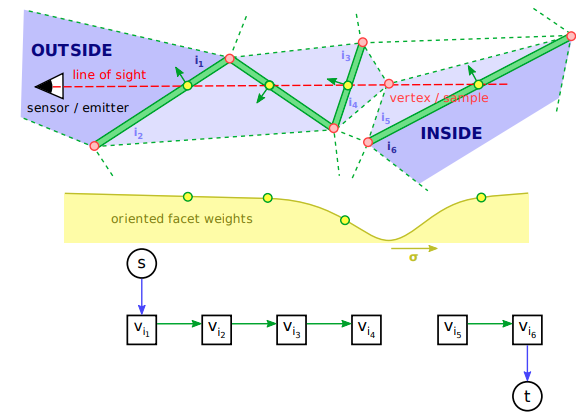
    • Surface quality: the quality of surface triangle is evaluated as the ratio of the length of their longest edge over the length of their shortest edge (minus one). And Soft 3D beta–skeleton in graph-cut algorithm.

    Efficient multi-view reconstruction of large-scale scenes using interest points, Delaunay triangulation and graph cuts 2007. First to consider surface visibility! the upper paper improved this method.

    Poisson Surface Reconstruction 2006 State-of-art.

    A mesh reconstruction algorithm driven by an intrinsic property of a point cloud 2004. It classfies meshing into the following methods :

    • sculpting-based approaches: Delaunay.
    • contour-tracing approaches: matching cube, Hhoppe’s.
    • region-growing approaches: (this paper) keep growing from inital triangulate.

    Mesh Optimization 1993, paper. This a very important milestone paper for 3d reconstruction. Its first section - Mesh representation - worth carefully read. It treat the problem as optimization, using a two step greedy method to solve.

    • Energy function is : $E = E_{distance} + E_{representation} + E_{spring}$ (see more details in the paper)
    • step 1. keep mesh structure, optimize vertices’ positions to best fit points.
    • step 2. keep vertices’ poitions, update mesh structure by three types of updat : edge collapse, edge split or edge swap, to simplify the mesh.

    Surface Reconstruction from Unorganized Points 1992. This a very important milestone paper for 3d reconstruction, you can found it is the basis of many modern methods. It finds a signed distance function, and use its tangent space to generate mesh.

    • using a local PCA to find local planes.
    • smoothen the planes (by the smoothness of the normals).
    • define signed distance by projecting points to local plane.
    • tracing its zero set, use a modified matching cube to generate mesh.

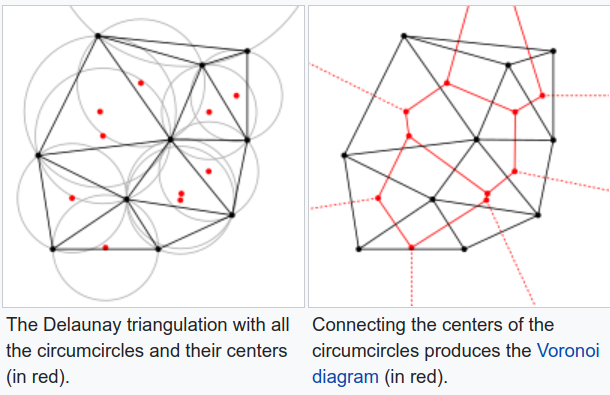
    Delaunay triangulation 1934: maximize the minimum of all the angles of the triangles in the triangulation. The Delaunay triangulation of a discrete point set P in general position corresponds to the dual graph of the Voronoi diagram for P