Table of Contents
2023
Wavemap : Efficient volumetric mapping of multi-scale environments using wavelet-based compression.
- measuremeent model : modeling the angular uncertainty and range uncertainty.
- Multi-Resolution Analysis - wavelet transformation
- Mapping comparison between wavemap and voxblox: resolution 5cm, 16 line lidar.
- wavemap could be a lot slower when resolution or size enlarged.
- wavemap result is more complete (fewer holes), but with larger wall width.
Point-LIO: Robust High-Bandwidth Lidar-Inertial Odometry.
- point-by-point update -> high frequency & high bandwidth.
- stochastic process model to estimate imu -> handle aggressive motions (imu saturation).
2022
Scale-Variant Robust Kernel Optimization for Non-linear Least Squares Problems (applied in LIO system to prevent outliers) use Generalized loss function in LIO slam system. As the paper itself said, it does not has obvious improvement on LIO system. I had tested different robust loss functions also in FAST-LIO system, no improvement found.
LITERATURE REVIEW (robust estimation):
- Iterative Re-weighted Least Squares (IRLS) : M-estimators, fails into de-weighting (don’t directly remove measurements). (connection to elliptical distributions), Student-t M-estimators. (M-estimation can be solved exactly like a weighted nonlinear least squares problem)
- loop closures: Dynamic Covariance Scaling, AEROS.
Efficient and Consistent Bundle Adjustment on Lidar Point Clouds, following work of BALM, github. (similar to global ICP method)
- Formulates the lidar BA problem based on edge and plane features.
- reduce to pose optimization problem (since the min loss of each observation depends only on pose).
- Summarizes all points of each scan associated to one feature by covariance (to reduce computational complexity).
- instead of enumerate each point separatly.
2021
LT-mapper: A Modular Framework for LiDAR-based Lifelong Mapping, github. multi-session mapping focus on environmental changes by alignment error.
- map fusion using Scan Context and radius search.
- us Removert for High Dynamic (HD) Points Removal & Low Dynamic (LD) Change Detection.
- PD (positif diff) removal & ND (negatif diff) merging. (Handle long-term scene change).
- (I think a well designed ray tracing could solve all the problems)
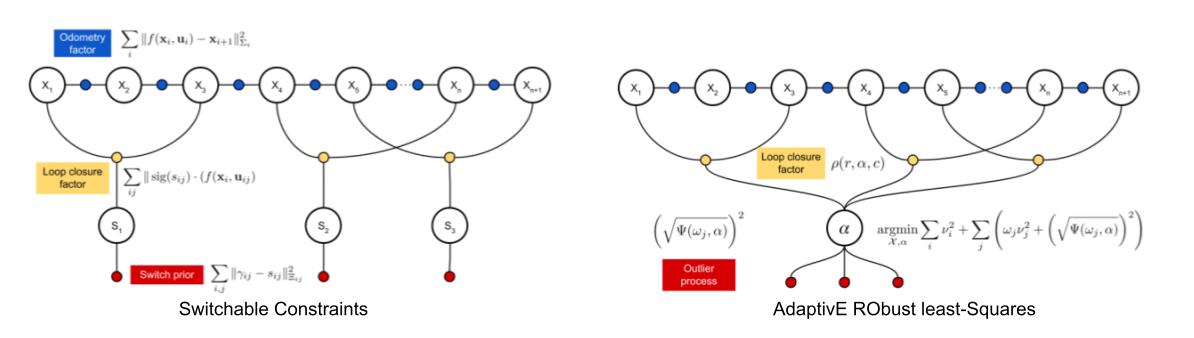
AEROS: AdaptivE RObust least-Squares for Graph-Based SLAM modelled all loop closures using robust cost functions with a single adaptive parameter and improved back end optimization. Take advantage of the Black-Rangarajan duality to convert the optimization problem into an Iteratively Reweighted Least Squares (IRLS) problem instead (similar to robust loss function in ceres).
Globally Consistent 3D LiDAR Mapping with GPU-accelerated GICP Matching Cost Factors, nice youtube video 1, nice youtube video 2 : minimizes matching costs (voxel data association-based GICP) between frames over the entire map using gpu.
- local maps
- global mapping : align local maps.
- use shifted Tukey robust kernel to escape from local minima.
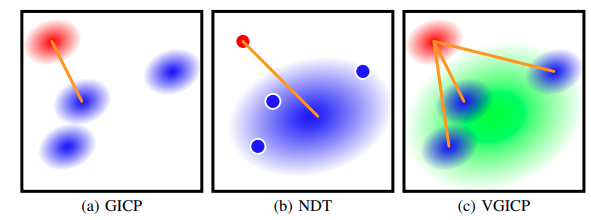
Voxelized GICP for Fast and Accurate 3D Point Cloud Registration voxelized generalized
iterative closest point (VGICP) (better fit gpu).
ERASOR: Egocentric Ratio of Pseudo Occupancy-based Dynamic Object Removal for Static 3D Point Cloud Map Building project map points and the new frame points into 2d gird, and compute the height range for each grid, use it to filter grid with moving object (for an example, if the range in map is 2 meter, while 10cm in new frame, it means the map gird might be moving objects). It looks very simple, while it is effective, worth adding to your own project.
MULLS: Versatile LiDAR SLAM via Multi-metric Linear Least Square.
- Lidar only slam (it doesn’t addition information (e.g. imu) for undistortion.)
- Use many kind of features (ground, facade, pillar, beam, etc) to make the system versatile. (and doesn’t depends on additional info for cloud, e.g ring).
- Registration to a local submap. solve the new ICP problem based on TEASER (applying truncated least square estimation with semi-definite relaxation).
- Process a loop closure and a pose graph optimization.
BALM: Bundle adjustment for lidar mapping . But the main results shown for Livox Device (denser, small FOV).
- Adaptive voxelization to match both plane and edge features without a segmentation.
- Reduce to pose only BA.
LiTAMIN2: Ultra Light LiDAR-based SLAM using Geometric Approximation applied with KL-Divergence. Using a covariance based ICP error, combined with a covariance shape error term (from KL divergence), which allow matching with very large voxel size, then making the registration extremely fast.
Range Image-based LiDAR Localization for Autonomous Vehicles.
- Passion reconstruction get mesh. (small in memory)
- Monte Carlo localization of lidar map. (particle filter with rendered range image)
LiLi-OM (LIvox LiDAR-Inertial Odometry and Mapping
- tightly-coupled idar-IMU hierarchical lide-window optimization.
- factors : imu-preint, lidar plane/edge pairs, prior/marginalization terms.
- conventional LiDARs : LOAM feature; solid-state LiDAR : use covariance.
FAST-LIO (Fast LiDAR-Inertial Odometry keyword : FAST, in my personal opinion, this is the state of art of lidar slam.
- EKF for imu, used to lidar undistortion.
- ikd-Tree (incremental kdtree) for lidar match.
my implementation, wonderful performance!
ikd-Tree: An Incremental K-D Tree for Robotic Applications, github. Dynamically insert/delete points, and re-balance the tree.
- in my test, it is slower to search nearest then nanoflann version. while it does not require rebuild every update.
2020
LIO-SAM Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In short, add imu pre-integration and sliding window to LOAM.
OverlapNet: Loop Closing for LiDAR-based SLAM. Top-down 2d view of lidar scan (with other info) for predict overlap rate and yaw.
ISC (Intensity Scan Context Coding Intensity and Geometry Relations for Loop Closure Detection. Encode lidar frame using geometry and intensity info (project intensity into ring distributed subspaces). Simple algorithm, shows wonderful result in experiment.
Remove, then Revert: Static Point cloud Map Construction using Multiresolution Range Images
(1) compare query and map range image to get dynamic point cloud. (2) process the division iteratively.
2019
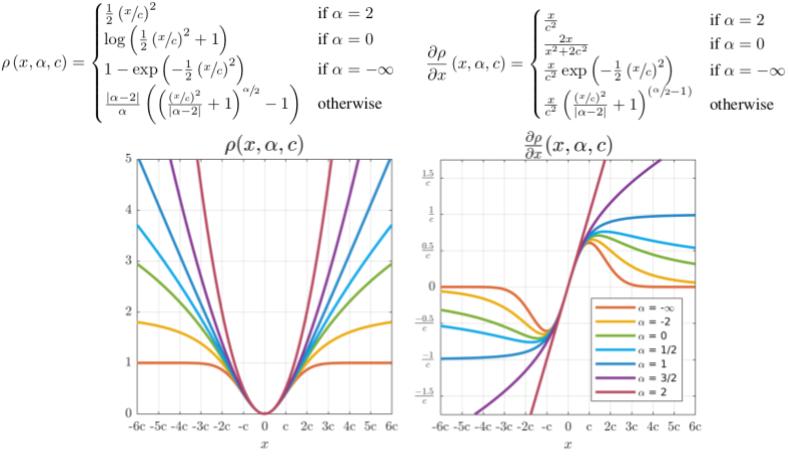
A General and Adaptive Robust Loss Function enables the training of neural networks in which the robustness of the loss auto-matically adapts itself during training.
2018
Efficient Surfel-Based SLAM (SuMa) using 3D Laser Range Data in Urban Environments Depth image based dense direct odometry : use the projective data association between the current scan and a rendered model view from that surfel map.
LeGO-LOAM. Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. See details and some comparisons.
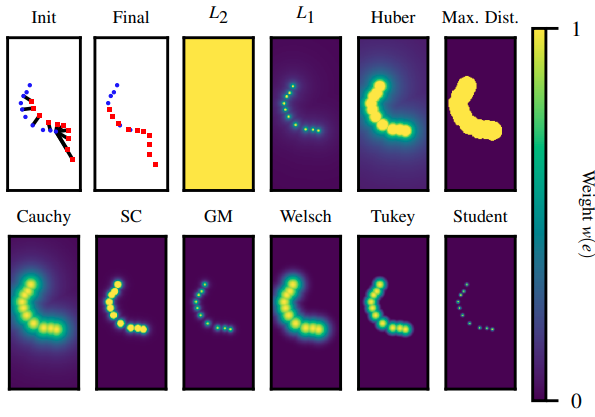
Analysis of Robust Functions for Registration Algorithms importance of M-estimators in ICP problems.
- that most outlier filters have similar performance if they are correctly tuned
- Var. Trim., Cauchy, and Cauchy MAD(Median of Absolute Deviation) are more stable against different environment types.
- Norm L1 produces comparable accuracy, while been parameterless.
2017
On the performance of metrics to predict quality in point cloud representations. Using absolute category rating (ACR) and able to perceive distortions.
On Subjective and Objective Quality Evaluation of Point Cloud Geometry. Point cloud quality metric using DSIS (double-stimulus impairement scale) methodology. Showing that current state-of-the-art objective metrics (point-to-point, point-to-plane or point-to-mesh) do not predict well visual quality, especially under typical distortions such as compression.
2D SLAM Quality Evaluation Methods. The proportion of occupied and free cells (check wall blurry). The amount of corners and enclosed areas in a map.
Detecting glass in simultaneous localisation and mapping, used in Cartographer glass. The received rays’ intensity will have the highest strength when the robot is receiving laser rays from the normal incident angle.
Earlier
Self-tuning M-estimators 2015. Robust least squares is equivalent to maximum-likelihood estimation with elliptically contoured data. One of the advantages of this interpretation is that it enables us to transform the original, non-convex problem into a series of iteratively re-weighted convex sub-problems. This is accomplished via the EM algorithm (Expectation-Maximization).
Robust Loop Closing Over time for Pose Graph SLAM 2013 Realizing, Reversing and Recovering (RRR), which clustered the pose graph edges, i.e. constraints consistent with one another (correct loop closures tend to agree among themselves and with the sequential constraints, while incorrect ones do not), using the place recognition constraints.
Robust map optimization using dynamic covariance scaling 2013 faster version of Switchable Constraints (up to a factor of 10). use a closed form solution for computing the scaling factors individually for each loop closing constrain (instead of adding optimization variable) : $s = \min(1, \frac{2\Phi}{\Phi + \xi_{l}^{2}})$, shows it is an extension of iterative re-weighted least squares (IRLS) and
robust M-Estimation : $w(x) = \frac{1}{1 + x^{2}}$. Worth a Try!
Switchable Constraints for Robust Pose Graph SLAM 2012, add a inlier/outlier indicator parameter for each factor. Tried this in our projects, EXTREMELY EFFICTIVE!
OctoMap 2012. Probabilistic representation, Modeling of unmapped areas, Efficiency (octree).
- point-to-point ICP: $T = argmin_{T}(\sum_{i}w_{i} | T b_{i} - m_{i} |^{2})$ with $C_{i}^{B}=I$ and $C_{i}^{A} = 0$
- point-to-plane ICP: $T = argmin_{T}(\sum_{i}w_{i} | \eta_{i} (T b_{i} - m_{i}) |^{2})$ with $C_{i}^{B}=P_{i}^{-1}$ and $C_{i}^{A} = 0$
- generalized ICP :
On Measuring the Accuracy of SLAM Algorithms 2009. (RPE vs APE) A metric that operates only on relative geometric relations between poses along the trajectory of the robot.