Table of Contents
理性:
- 第一层,说理理性,reason——论证。
- 第二层,推理理性,作为前提的理由足以推导出作为结论的主张,reasonableness——推理。
- 第三层,合理性,追求价值平衡,rationality——哲学。
本书内容——回归实践、导论性:
- 演绎逻辑:词项逻辑、命题逻辑、谓词逻辑。
- 归纳逻辑。
- 非形式逻辑:谬误理论为主。
1. 引论
把逻辑学理解为“研究推理形式中有效性的科学”(狭义逻辑学)的观点过于狭隘,在广义逻辑学上看,逻辑学是研究如何把好的推理或论证与不好的推理或论证区别开来的科学,也就是关于推理或论证的科学。
1.1 简史
(1)亚里斯多德。
(2)莱布尼茨之梦,两个基本假定:
- 我们的思想由非常少量的简单思想复合而成,而这些简单思想形成了人类思想的字母系统。
- 复杂思想都是从这些简答思想通过统一的对称组合开始的,而且这些组合与运算相似。
(3)罗素,怀海特《数学原理》。想要说明数学整体上是从逻辑的前提推导出来的,并尝试只用逻辑定义数学概念,同时尽量找出逻辑本身的所有原理,提出了数学基础的逻辑主义方案。
(4)哥德尔“不完全定理”,数学的“完备性”和“一致性”不能同时拥有。
- 哥德尔第一不完全性定理:任意一个包含算术系统在内的形式系统中,都存在一个命题,它在这个系统中既不能被证明也不能被否定。
- 哥德尔第二不完全性定理:任意一个包含算术系统的形式系统不能证明它本身的一致性。
1.2 逻辑学本质
逻辑形式(logical form):(1)忽略词性、词缀等与逻辑不相干的语法特征,用逻辑语言替换日常语言。(2)用示意性符号取代语句中某些(具体的)成分。传统形式逻辑标准命题由四个部分组成(1)量词;(2)主项;(3)联项;(4)谓项,只会涉及少数几个逻辑连接词,而且只允许一个量词来管辖推论(“所有人都会死”——“有些人拥有所有运气”)。而现代形式逻辑,简单命题的基本形式是通过递归形式给出的,其中涉及逻辑连接词。
- 传统形式逻辑:亚里斯多德的词项逻辑(三段论逻辑)、斯多葛命题逻辑。
- 命题逻辑:表达命题的公式能够通过用逻辑连接词将原子命题组织而成,而且一个形式证明规则系统允许某个公式被作为“定理”来确立。
- 现代形式逻辑:试图用形式系统——形式语言、推演规则、公理组成——来把握逻辑真理或逻辑推论的本质。
- 数理逻辑:符号逻辑的扩充。(1)形式逻辑技术在数学推理中的应用;(2)数学技术应用于形式逻辑的分析和表示。(命题演算、谓词演算、模型论、递归论、证明论、集合论等)
- 谓词逻辑:一阶逻辑、二阶逻辑、多类逻辑或无穷逻辑等符号形式系统的总称。弗雷德、希尔伯特、阿克曼。
- 一阶逻辑(命题演算和谓词演算):能够被通过添加一个一阶递归命题集作为公理将其公理化为一阶逻辑的扩充。足以形式化集合论的全部,本质上可以形式化全部数学。但是它把量化限制在了个体上,能以用于拓扑目的。
非形式逻辑:研究自然语言论证的逻辑,其对象是非形式推理的分析、评价与构建。
- 论辩逻辑(dialectical logic):关注通过逻辑推理达到结论——以前提为基础的。
- 谬误逻辑。
演绎推理(deductive reasoning)——必然性推理,关注的是从给定前提必然推导出结论。可以给出推理的(绝对的)有效性。
归纳推理(inductive reasoning)——或然性推理,是一个根据经验观察推演出一个可信概括的过程。由于难以穷举所有现实经验可能,这里包含了数学概率模型。
四大定理:
- 一致性定理:逻辑系统内的定理不能相互矛盾。
- 有效性定理:逻辑系统的证明规则不会允许从真前提推导出假结论。公式、命题、论证的有效性。
- 可靠性定理:逻辑系统的证明规则不会允许从帧前提推导出假结论,而且前提已被证明为真。逻辑系统的可靠、论证的可靠性。
- 完全性定理(完备性):不存在逻辑系统内原则上不能证明的真命题。
1.3 主要争论
(1)二值原则与排中律问题。二值原则:命题p或者是真的或者是假的。发展到第三值“可能”——模态逻辑(非经典逻辑)——概率系统。
(2)实质蕴涵问题。实质蕴涵:表达特定条件性质。实质蕴涵怪论:在经典逻辑中为真但直观上又有问题的公式(结论的正确性,不依赖于前提条件)。严格蕴涵,遵照来自模态逻辑的必然性算子行事的实质条件。
(3)逻辑是经验吗?
(4)不一致性能容忍吗?应该容忍,相干逻辑与超协调逻辑。黑格尔辩证法中,矛盾律与同一律本身依赖于差异性(依赖于环境条件),其本身不是独立可断定的。莱布尼茨要求充足理由律——任何判断必须有(充足)理由。
(5)逻辑真理可拒斥吗?(怀疑论):逻辑依赖于不与现实世界中的任何东西相符的假定。
我的想法:逻辑学的内容大部分还是形式的(比如各种严格的定义、各种严格的分类),但是它的形式又不如自然科学那么先验(虽然自然科学也可能不是先验的),或者说它的定义、分类和形式更加依赖于经验(比如它的定义,不同的思想家可以有不同的定义——依赖于不同思想家的经验,而不像自然科学能够共享定义——似乎含有更多的普遍性)。所以这种很依赖于经验,客观性逊色于自然科学的形式科学,就会让人感觉到违和感。
2. 论证
2.1 论证的概念
推论(inference)从前提推导出结果的行为或过程,是一个命题序列,其中一个命题被称为结论,其余命题被称为前提;推理(reasoning)是一个推论序列;论证(argument)是一个推理序列。
命题(proposition)和陈述(statement)都是表明真或不真的语句(sentence)。命题必须要有恰当的语法字符串,而且必须有真假的判断。
- 经验命题:根据经验判断
- 必然命题:不需要经验,总是为真或假(比如重言式、矛盾式命题)。
论证(argument),演绎论证、归纳论证、似真论证(协同论证,plausible——标准是模糊的似真)。论辩功能:证成、反驳、说服。
- as product(结果,“生产”): 前提(premise)-> 结论(conclusion)。形式的。
- as proceduce: 理由(reason)-> 主张(claim)。论辩的。
- as process:强调过程和程序。修辞的。“论证者为自己的主张(结论)提出理由(前提)并试图说服目标听众接受该主张的过程和结果”。
2.2 识别论证
论证三要素:(1)前提与结论(形式逻辑关注的对象);(2)论证者与目标听众;(3)论证的目的(2,3往往是隐性的)。
论证结构(structure):简单结构、序列结构、收敛结构、闭合结构、发散结构。 论证形式(form),只关心简单和闭合结构,因为其他的结构都可以分解为简单、闭合的组合。
解释(explanation),描述一个事实并对这个事实的原因进行说明,而并非前提支撑结论的结构。
我的想法:识别论证的元素或者与解释区分,在没有标志性词语的情况下都是看语境的。这也同时说明了逻辑的前提是我们的感性生活,是一些非理性的东西。我们需要用批判的眼光看逻辑论证,一方面从具体的事情中总结出抽象的规则,但是又不能忘记这些抽象规则的前提正是具体的生活。
2.3 论证评价的标准
逻辑标准(分析标准):(1)演绎逻辑标准(论证的可靠性必然性——前提为真且推理形式有效);(2)归纳逻辑标准(归纳强度——概率);(3)非形式逻辑标准(结合了具体内容的:前提都可以接受——考虑到具体情况的“真”;前提与结论相关;前提对结论提供了充分支持)。
修辞标准:好的——它对于目标听众来说是可接受的。修辞术的发展。
论辩标准:好的——它是通过理性方式消除了意见分歧。
3. 直言命题逻辑
the logic of categorical proposition, term logic。对当关系论证、直言命题运算论、三段论。
直言命题(范畴命题categorical proposition):陈述句;反映两对象关系。
- 分类。A:全称肯定命题;E:全称否定命题;I:特称肯定命题;O:特称否定命题。
- 要素:量项(universal/particular)、主项(Subject)、联项(copula)、谓项(Predicate)。
- 周延性:主/谓为全称时,全称的主项是周延的,否定的谓项是周延的。S在AE中周延,P在EO中周延。
- 文恩图(John Venn)、欧拉图:表示主谓关系。
3.1 对当关系论证
一个命题的真假能否推出另一个命题的真假。
- 假设观点:对主谓的存在不作假定,可以为空集(并非现实中的存在,而仅仅是假设的前提集合是否为空)——矛盾关系。
- 存在观点:主谓不能为空集——矛盾、反对、下反对、蕴涵关系。
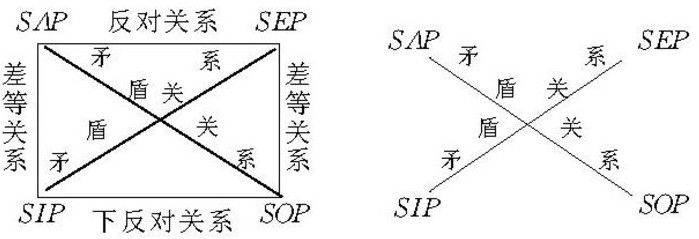
- 矛盾关系:相同主谓、不同量质——不能同真、不能同假。8种有效形式。
- 反对关系:(A-E)相同主谓、全称、不同的质——不能同真、但可同假。2种有效形式。
- 下反对关系:(I-O)相同主谓、特称、不同的质——可以用真、不能同假。2种有效形式。
- 蕴涵关系(等差关系):(A-I,E-O)相同主谓、不同的量,相同的质——既可同真、又可同假。4种有效形式。
3.2 直言命题运算论证
一个命题能否推出另一个命题。直言命题运算:改变命题的质或/和量。逻辑等值与逻辑独立(——covariance)。
- 换位法:交换命题的主谓,保持其他部分不变。E、I在换位下逻辑等值。$SAP\implies PIS$、$SEP\implies PES$、$SIP\implies PIS$。
- 换质法:改变命题的质,通常否定谓项,其他不变。所有命题在换质下逻辑等值。$SAP\implies SE\bar{P}$、$SEP\implies SA\bar{P}$、$SIP\implies SO\bar{P}$、$SOP\implies SI\bar{P}$。
- 对换法:交换主谓、同时否定主谓、其他不变。A、O在对换下逻辑等值。$SAP\implies \bar{P}A\bar{S}$、$SOP\implies \bar{P}O\bar{S}$。
3.3 直言三段论
定义:(1)包含三个标准形式的直言命题——两个前提、一个结论;(2)共有三个不同的主谓项;(3)每个项在不同命题中出现两次。
基本形式举例:
- major premise:M(middle term)- P(major term)。
- minor premise:S(minor term)- M(middle term)。
- 所以,S(minor term)- P(major term)。
三段论的格:
- 第一格:$MAP, SAM \therefore SAP$。
- 第二格:$PAM, SAM \therefore SAP$。
- 第三格:$MAP, MAS \therefore SAP$。
- 第四格:$PAM, MAS \therefore SAP$。
三段论的规则(假设的观点来看需要全部,存在的观点来看只需要1-4条):
- 中项(M)必须至少周延一次。
- 前提中不周延的项,在结论中不得周延。大项不当周延/小项不当周延。
- 不能有两个否定前提。
- 前提中有一个是否定命题 $\Leftrightarrow$ 结论是否定命题。
- 不能有两个全称前提和一个特称结论。
论证重构为标准的三段论:非标准直言命题重构;非标准三段论重构。
4. 真值函项逻辑
4.1 复合命题论证
研究复合命题(包含了一个或一个以上较短命题作为其自身一部分成分的命题,借助逻辑联结词——否定、析取、合取、条件——组合)的分析和评价——命题演算。
- 否定论证:只有一个前提和结论,前提或结论带有否定联结词,但不能都带有两个否定联结词(p->非非p,非非p->p)。
- 合取论证:前提或结论中有一个为合取命题(或称联言命题,断定两个对象可能性同时存在/同时为真的复合命题,$p \land q$)。
- 析取论证:由两个前提组成,其中一个前提是析取命题(或称选言命题,断定两个或以上对象至少有一个存在或为真,$p \lor q$),另一个前提是对其中一个析取支进行否定/肯定的论证。
- 条件论证:广义——充分/必要/充要,狭义——充分(蕴涵)。
- 二难论证(dilemma):或称假言选言推理——两个条件命题、一个二支析取和一个结论组成的论证。
4.2 真值函项
复合命题的真假是其支命题真假的一个函项。
联结词:否定($\lnot$)、合取($\land$)、析取($\lor$)、条件($\to$)、等值($\equiv$、$\leftrightarrow$)。括号的帮助。
真值表:枚举所有可能性组合。
- 用来判断命题的“蕴涵”——逻辑蕴涵(logical implication)、实质蕴涵(material implication)——A命题为真则B命题的枚举可能性都为真的情况。
- 用来判断命题的等值——所有枚举都一致。
- 用来判断论证的有效性——前提为真则结论为真。判断论证是重言(结论必定为真)或矛盾(结论必定为假)。
4.3 形式演绎
对论证有效性的形式证明。一步步分解检查证明的流程,这里进一步把基本的推理分解总结成公式。 证明有效性的间接方法:归谬法(反证法)。证明无效性的简便证明法:寻找反例。
5. 量化逻辑
量化符号:
- 存在量化。把特称的主词符号化为变元x,并且用存在$\exists x$描述。
- 全称量化。把全称的主词符号化为变元x,并且用存在$\forall x$描述。
直言命题符号化(其中SP是谓词):
- A:$(x)(Sx\to Px)$
- E:$(x)(Sx\to \lnot Px)$
- I:$(\exists x)(Sx \lor Px)$
- O:$(\exists x)(Sx \lor \lnot Px)$
论证的有效性证明:
- 全程例示规则(Universal Instantiation),由全称到个例的推导,$(x)Hx \to Ha$。
- 存在例示规则(Existential Instantiation),由存在量化命题推导出其至少一个具体事例,$(\exists x)Fx \to Fa$。
- 量化等值规则:(1)$\lnot(x)… \to (\exists x)\lnot…$;(2)$\lnot(\exists x)… \to (x)\lnot…$;(3)全称析取式,$(x)… \leftrightarrow (x)…$;(4)存在析取式,$(\exists x)… \leftrightarrow (\exists x)…$。
一般量化:一元量化的拓展。
6. 归纳推理
诉诸感觉经验的,概率的。
- 归纳概括:基于具体观察做出的概括性陈述,给出一个一般性命题。
- 归纳类比(analogy):基于其他相似的东西,做出的单称命题判断。
- 因果假设:用来探求因果联系的逻辑方法。培根“三表法”的基础上,弥尔”五法:求同法、求异法、求同求异并用法、共变法、剩余法。
解释性假设——假说。提出与结论相匹配的解释。
7. 谬误
谬误(fallacy):看起来让人相信但实际上并不是逻辑上可靠的推理或论证——逻辑上有缺陷的。
前提谬误:
- (前提)不一致谬误——所有前提必须同时可以接受。
- 前提不可接受:前提虚假、预期理由谬误(有待被证实)、自相矛盾谬误——每个前提必须可以接受。
- 乞题谬误:循环论证——前提的可接受性不得依赖于结论的可接受性。
不相干谬误:
- 不相干结论:转移论题(不故意)、偷换论题(故意)、稻草人谬误(曲解/偷换对方的论题)——结论必须与前提相干。
- 不相关前提:人身攻击谬误、诉诸权威谬误、诉诸情感谬误(公众、威力、怜悯)、诉诸无知谬误、诉诸传统谬误——前提必须与结论相干。
支持谬误:
- 支持谬误:无效、归纳不强的论证——前提必须给结论提供充分支持。
- 合成谬误:(把组成部分、个体的结论,“合成”到整体、总类上)
- 一个关于整体的结论是以其构成要素的性质为前提推导出来的,而实际上以这些要素的性质为前提却推导不出这个关于整体的结论的。
- 一个关于对象类的结论是以其组成类的个体成员的性质为前提推导出来的,而实际上这些个体成员的性质为前提是推导不出这个关于对象类的结论的。
- 分解谬误:与合成谬误相对应。
- 以先后定因果谬误。